4.1.4 APLICACIONES

Un árbol binario es una estructura de datos útil cuando se trata de hacer modelos de procesos en donde se requiere tomar decisiones en uno de dos sentidos en cada parte del proceso. Por ejemplo, supongamos que tenemos un arreglo en donde queremos encontrar todos los duplicados. Esta situación es bastante útil en el manejo de las bases de datos, para evitar un problema que se llama redundancia.

Una manera de encontrar los elementos duplicados en un arreglo es recorrer todo el arreglo y comparar con cada uno de los elementos del arreglo. Esto implica que si el arreglo tiene   elementos, se deben hacer  comparaciones, claro, no es mucho problema si   es un número pequeño, pero el problema se va complicando más a medida que   aumenta. Si usamos un árbol binario, el número de comparaciones se reduce bastante, veamos cómo.

El primer número del arreglo se coloca en la raíz del árbol (como en este ejemplo siempre vamos a trabajar con árboles binarios, simplemente diremos árbol, para referirnos a un árbol binario) con sus subárboles izquierdo y derecho vacíos. Luego, cada elemento del arreglo se compara son la información del nodo raíz y se crean los nuevos hijos con el siguiente criterio:

•        Si el elemento del arreglo es igual que la información del nodo raíz, entonces notificar duplicidad.

•        Si el elemento del arreglo es menor que la información del nodo raíz, entonces se crea un hijo izquierdo.

•        Si el elemento del arreglo es mayor que la información del nodo raíz, entonces se crea un hijo derecho.

4.1.5 ARBOLES BALANCEADOS AVL.

La estructura de datos más vieja y mejor conocida para árboles balanceados es el árbol AVL. Su propiedad es que la altura de los subárboles de cada nodo difiere en no más de1. Para mantenerlo balanceado es necesario saber la altura o la diferencia en alturas de todos los subárboles y eso provoca que tengamos que guardar información adicional en cada nodo, un contador de la diferencia entre las alturas de sus dos subárboles.

Los árboles AVL fueron nombrados por sus desarrolladores Adel' son-Vel'skii y Landis.

Probablemente la principal característica de los árboles AVL es su excelente tiempo de ejecución para las diferentes operaciones (búsquedas, altas y bajas).

En las siguientes dos figuras la primera es un árbol AVL y la segunda no lo es ya que los subárboles del nodo 'L' difieren en altura por más de 1.

Árbol AVL: El árbol a es un árbol AVL, mientras que el árbol b no lo es

 

 

Rotaciones simples de nodos
Los reequilibrados se realizan mediante rotaciones, en el siguiente punto veremos cada caso.
Rotación simple a la derecha (SD):
Esta rotación se usará cuando el subárbol izquierdo de un nodo sea 2 unidades más alto que el derecho, es decir, cuando su FE sea de -2. Y además, la raíz del subárbol izquierdo tenga una FE de -1, es decir, que esté cargado a la izquierda.

Procederemos del siguiente modo:
Llamaremos P al nodo que muestra el desequilibrio, el que tiene una FE de -2. Y llamaremos Q al nodo raíz del subárbol izquierdo de P. Además, llamaremos A al subárbol izquierdo de Q, B al subárbol derecho de Q y C al subárbol derecho de P.

En el gráfico que puede observar que tanto B como C tienen la misma altura (n), y A es una unidad mayor (n+1). Esto hace que el FE de Q sea -1, la altura del subárbol que tiene Q como raíz es (n+2) y por lo tanto el FE de P es -2.
1. Pasamos el subárbol derecho del nodo Q como subárbol izquierdo de P. Esto mantiene el árbol como ABB, ya que todos los valores a la derecha de Q siguen estando a la izquierda de P.
2. El árbol P pasa a ser el subárbol derecho del nodo Q.
3. Ahora, el nodo Q pasa a tomar la posición del nodo P, es decir, hacemos que la entrada al árbol sea el nodo Q, en lugar del nodo P. Previamente, P puede que fuese un árbol completo o un subárbol de otro nodo de menor altura. 

En el árbol resultante se puede ver que tanto P como Q quedan equilibrados en cuanto altura. En el caso de P porque sus dos subárboles tienen la misma altura (n), en el caso de Q, porque su subárbol izquierdo A tiene una altura (n+1) y su subárbol derecho también, ya que a P se añade la altura de cualquiera de sus subárboles.

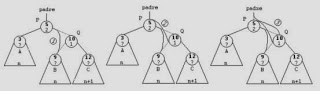
Rotación simple a la izquierda (SI):
Se trata del caso simétrico del anterior. Esta rotación se usará cuando el subárbol derecho de un nodo sea 2 unidades más alto que el izquierdo, es decir, cuando su FE sea de 2. Y además, la raíz del subárbol derecho tenga una FE de 1, es decir, que esté cargado a la derecha.

Procederemos del siguiente modo:
Llamaremos P al nodo que muestra el desequilibrio, el que tiene una FE de 2. Y llamaremos Q al nodo raíz del subárbol derecho de P. Además, llamaremos A al subárbol izquierdo de P, B al subárbol izquierdo de Q y C al subárbol derecho de Q.

En el gráfico que puede observar que tanto A como B tienen la misma altura (n), y C es una unidad mayor (n+1). Esto hace que el FE de Q sea 1, la altura del subárbol que tiene Q como raíz es (n+2) y por lo tanto el FE de P es 2.
1. Pasamos el subárbol izquierdo del nodo Q como subárbol derecho de P. Esto mantiene el árbol como ABB, ya que todos los valores a la izquierda de Q siguen estando a la derecha de P.
2. El árbol P pasa a ser el subárbol izquierdo del nodo Q.
3. Ahora, el nodo Q pasa a tomar la posición del nodo P, es decir, hacemos que la entrada al árbol sea el nodo Q, en lugar del nodo P. Previamente, P puede que fuese un árbol completo o un subárbol de otro nodo de menor altura.

En el árbol resultante se puede ver que tanto P como Q quedan equilibrados en cuanto altura. En el caso de P porque sus dos subárboles tienen la misma altura (n), en el caso de Q, porque su subárbol izquierdo A tiene una altura (n+1) y su subárbol derecho también, ya que a P se añade la altura de cualquiera de sus subárboles.