viernes, 1 de noviembre de 2013
Unidad 4 Estructuras no lineales
Caso base: un árbol con sólo un nodo (es a la vez raíz del árbol y hoja).
El recorrido en inorden, también llamado orden simétrico (aunque este nombre sólo cobra significado en los árboles binarios) consiste en recorrer en primer lugar A_1, luego la raíz y luego cada uno de los hijos A_2 \dots A_k en orden simétrico.
4.1 Arboles
4.1.1 Concepto de árbol
4.1.2 Clasificación de arboles
4.1.3 Operaciones básicas sobre arboles binarios
4.1.4 Aplicaciones
4.1.5 Arboles balanceados (AVL)
4.2 Grafos
4.2.1 Terminología de grafos
4.2.2 Operaciones básicas sobre grafos.
4.1 ARBOLES
Un árbol es una estructura no lineal en la que cada nodo puede apuntar a uno o varios nodos.
También se suele dar una definición recursiva: un árbol es una estructura en compuesta por un dato y varios árboles.
Esta estructura se usa principalmente para representar datos con una relación jerárquica entre sus elementos, como por ejemplo registros, árboles genealógicos, y tablas de contenidos. Vamos a profundizar en un tipo especial de árbol llamado árbol binario, la cual puede ser implementada fácilmente en la computadora; aunque en un árbol puede parecer muy restrictivo. También se va a ampliar sobre árboles más generales y puntos con relación a los árboles binarios; entre estos tenemos a la terminología, los árboles binarios complementos, árboles binarios de búsqueda, búsqueda e inserción en árboles binarios de búsqueda, árboles generales, representación de árboles generales en la computadora y correspondencia entre los árboles generales y árboles binarios.
4.1.1 CONCEPTO DE ARBOLES
Caso base: un árbol con sólo un nodo (es a la vez raíz del árbol y hoja).
Una sucesión de nodos del árbol, de forma que entre cada dos nodos consecutivos de la sucesión haya una relación de parentesco, decimos que es un recorrido árbol. Existen dos recorridos típicos para listar los nodos de un árbol: primero en profundidad y primero en anchura. En el primer caso, se listan los nodos expandiendo el hijo actual de cada nodo hasta llegar a una hoja, donde se vuelve al nodo anterior probando por el siguiente hijo y así sucesivamente. En el segundo, por su parte, antes de listar los nodos de nivel n+1 (a distancia n+1 aristas de la raíz), se deben haber listado todos los de nivel n. Otros recorridos típicos del árbol son preorden, postorden e inorden:
El recorrido en inorden, también llamado orden simétrico (aunque este nombre sólo cobra significado en los árboles binarios) consiste en recorrer en primer lugar A_1, luego la raíz y luego cada uno de los hijos A_2 \dots A_k en orden simétrico.
El recorrido en postorden, también llamado orden posterior consiste en recorrer en primer lugar cada uno de los hijos A_1, A_2 \dots A_k en orden posterior y por último la raíz.
4.1.2 CLASIFICACIÓN DE ÁRBOLES
- Arboles binarios:
Arboles cuyos nodos contienen dos enlaces (uno de los cuales puede ser null). El nodo raíz es el primer nodo de un árbol. Cada enlace en el nodo raíz hace referencia un hijo. El hijo izquierdo es el primer nodo en el subárbol izquierdo (también conocido como el nodo raíz del subárbol izquierdo). El hijo derecho es el primer nodo en el subárbol derecho (también conocido como el nodo raíz del subárbol derecho).Los hijos de un nodo especifico se llaman hermanos. Un nodo sin hijos se llama nodo hoja. Generalmente, los científicos computacionales dibujan arboles desde el nodo raíz hacia abajo; exactamente lo opuesto a la manera en que crecen los arboles naturales. Recorrido de un árbol binario:- Recorrido: Requiere que cada nodo del árbol sea procesado (visitado) una vez y solo en una secuencia predeterminada. Existen dos enfoques generales para la secuencia de recorrido, profundidad y anchura. Recorrido en profundidad:
El proceso exige un camino desde la raíz a través de un hijo, al descendiente más lejano del primer hijo antes de proseguir a un segundo hijo. En otras palabras, en el recorrido en profundidad, todos los descendientes de un hijo se procesaran antes del siguiente hijo.
Recorrido en anchura: El proceso se realiza horizontalmente desde el raíz a todos sus hijos, a continuación a los hijos de sus hijos y así sucesivamente hasta que todos los nodos han sido procesados. En otras palabras, en el recorrido en anchura cada nivel se procesa totalmente antes que comience el siguiente nivel.
- Arboles de búsqueda binaria:
(Sin valores de nodo duplicado) cuenta con la característica de que los valores en cualquier subárbol izquierdo son menores que el valor del nodo padre de ese subárbol, y el valores en cualquier subárbol derecho son mayores que el valor del nodo padre de ese subárbol.
El árbol de búsqueda binaria facilita la eliminación de valores duplicados. Al crear un árbol, la operación de inserción reconoce los intentos de insertar un valor duplicado, ya que este sigue las mismas decisiones de “ir a la izquierda” “ir a la derecha” en cada comparación, al igual que el valor original. Por lo tanto, la operación de inserción eventualmente compara el valor duplicado con un nodo que contenga el mismo valor.
Arboles estrechamente empaquetados (o balanceados):
En este tipo de arboles, cada nivel contiene cerca del doble de elementos que el nivel anterior.-
Arboles AVL: Están siempre equilibrados de tal modo que para todos los nodos, la altura de la rama izquierda no difiere en más de una unidad de la altura de la rama derecha o viceversa. Gracias a esta forma de equilibrio (o balanceo), la complejidad de una búsqueda en uno de estos árboles se mantiene siempre en orden de complejidad O (log n).
factor de equilibrio
puede ser almacenado directamente en cada nodo o ser computado a partir de las alturas de los sub árboles. Ejemplo:
- Arboles rojo negro:
Un árbol rojo-negro es un árbol binario de búsqueda en el que cada nodo tiene un atributo de color cuyo valor es o bien rojo o bien negro. Además de los requisitos impuestos a los árboles binarios de búsqueda convencionales, se deben satisfacer los siguientes para tener un árbol rojo-negro válido:
▪Todo nodo es o bien rojo o bien negro.
▪La raíz es negra.
▪Todas las hojas son negras (las hojas son los hijos nulos).
▪Los hijos de todo nodo rojo son negros (también llamada "Propiedad del rojo").
▪ Cada camino simple desde un nodo a una hoja descendiente contiene el mismo número de nodos negros, ya sea contando siempre los nodos negros nulos, o bien no contándolos nunca (el resultado es equivalente). También es llamada" Propiedad del camino", y al número de nodos negros de cada camino, que es constante para todos los caminos, se le denomina "Altura negra del árbol", y por tanto el camino no puede tener dos rojos seguidos. El camino más largo desde la raíz hasta una hoja no es más largo que 2 veces el camino más corto desde la raíz del árbol a una hoja en dicho árbol. El resultado es que dicho árbol está aproximadamente equilibrado.
- Árbol AA:
Los árboles AA son una variación del árbol rojo-negro, que a su vez es una mejora del árbol binario de búsqueda. A diferencia de los árboles rojo-negro, los nodos rojos en un árbol AA sólo pueden añadirse como un hijo derecho. En otras palabras, ningún nodo rojo puede ser un hijo izquierdo.
- Arboles multicamino:
Un árbol multicamino posee un grado g mayor a dos, donde cada nodo de información del árbol tiene un máximo de g hijo.
4.1.3 OPERACIONES BÁSICAS SOBRE ARBOLES BINARIO.
▪Enumerar todos los elementos.
▪Buscar un elemento.
.Dado un nodo, listar los hijos (si los hay).
▪Borrar un elemento.
▪Eliminar un subárbol (algunas veces llamada podar
▪Añadir un subárbol (algunas veces llamada injertar
▪Encontrar la raíz de cualquier nodo. Por su parte, la representación puede realizarse de diferentes formas. Las más utilizadas son: Advertisement
▪Representar cada nodo como una variable en el heap, con punteros a sus hijos y a su padre.
▪Representar el árbol con un array donde cada elemento es un nodo y las relaciones padre-hijo vienen dadas por la posición del nodo en el array.
4.1.4 APLICACIONES
Un árbol binario es una estructura de datos útil
cuando se trata de hacer modelos de procesos en donde se requiere tomar
decisiones en uno de dos sentidos en cada parte del proceso. Por ejemplo,
supongamos que tenemos un arreglo en donde queremos encontrar todos los
duplicados. Esta situación es bastante útil en el manejo de las bases de datos,
para evitar un problema que se llama redundancia.
Una manera de encontrar los elementos duplicados en
un arreglo es recorrer todo el arreglo y comparar con cada uno de los elementos
del arreglo. Esto implica que si el arreglo tiene elementos, se deben hacer comparaciones, claro, no es mucho problema
si es un número pequeño, pero el
problema se va complicando más a medida que
aumenta. Si usamos un árbol binario, el número de
comparaciones se reduce bastante, veamos cómo.
El primer número del arreglo se coloca en la raíz
del árbol (como en este ejemplo siempre vamos a trabajar con árboles binarios,
simplemente diremos árbol, para referirnos a un árbol binario) con sus
subárboles izquierdo y derecho vacíos. Luego, cada elemento del arreglo se
compara son la información del nodo raíz y se crean los nuevos hijos con el
siguiente criterio:
• Si el
elemento del arreglo es igual que la información del nodo raíz, entonces
notificar duplicidad.
• Si el
elemento del arreglo es menor que la información del nodo raíz, entonces se
crea un hijo izquierdo.
• Si el
elemento del arreglo es mayor que la información del nodo raíz, entonces se
crea un hijo derecho.
4.1.5 ARBOLES BALANCEADOS AVL.
La estructura de
datos más vieja y mejor conocida para árboles balanceados es el árbol AVL. Su
propiedad es que la altura de los subárboles de cada nodo difiere en no más
de1. Para mantenerlo balanceado es necesario saber la altura o la diferencia en
alturas de todos los subárboles y eso provoca que tengamos que guardar
información adicional en cada nodo, un contador de la diferencia entre las
alturas de sus dos subárboles.
Los árboles AVL
fueron nombrados por sus desarrolladores Adel' son-Vel'skii y Landis.
Probablemente la
principal característica de los árboles AVL es su excelente tiempo de ejecución
para las diferentes operaciones (búsquedas, altas y bajas).
En las siguientes
dos figuras la primera es un árbol AVL y la segunda no lo es ya que los
subárboles del nodo 'L' difieren en altura por más de 1.
Árbol AVL: El árbol a es un árbol AVL, mientras que el árbol b
no lo es
Rotaciones simples de nodosLos reequilibrados se realizan mediante rotaciones, en el siguiente punto veremos cada caso.
Rotación simple a la derecha (SD):
Esta rotación se usará cuando el subárbol izquierdo de un nodo sea 2 unidades más alto que el derecho, es decir, cuando su FE sea de -2. Y además, la raíz del subárbol izquierdo tenga una FE de -1, es decir, que esté cargado a la izquierda.
Procederemos del siguiente modo:
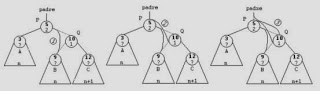
Llamaremos P al nodo que muestra el desequilibrio, el que tiene una FE de -2. Y llamaremos Q al nodo raíz del subárbol izquierdo de P. Además, llamaremos A al subárbol izquierdo de Q, B al subárbol derecho de Q y C al subárbol derecho de P.
En el gráfico que puede observar que tanto B como C tienen la misma altura (n), y A es una unidad mayor (n+1). Esto hace que el FE de Q sea -1, la altura del subárbol que tiene Q como raíz es (n+2) y por lo tanto el FE de P es -2.
1. Pasamos el subárbol derecho del nodo Q como subárbol izquierdo de P. Esto mantiene el árbol como ABB, ya que todos los valores a la derecha de Q siguen estando a la izquierda de P.
2. El árbol P pasa a ser el subárbol derecho del nodo Q.
3. Ahora, el nodo Q pasa a tomar la posición del nodo P, es decir, hacemos que la entrada al árbol sea el nodo Q, en lugar del nodo P. Previamente, P puede que fuese un árbol completo o un subárbol de otro nodo de menor altura.
Rotación simple a la izquierda (SI):
Se trata del caso simétrico del anterior. Esta rotación se usará cuando el subárbol derecho de un nodo sea 2 unidades más alto que el izquierdo, es decir, cuando su FE sea de 2. Y además, la raíz del subárbol derecho tenga una FE de 1, es decir, que esté cargado a la derecha.
Procederemos del siguiente
modo:Llamaremos P al nodo que muestra el desequilibrio, el que tiene una FE de 2. Y llamaremos Q al nodo raíz del subárbol derecho de P. Además, llamaremos A al subárbol izquierdo de P, B al subárbol izquierdo de Q y C al subárbol derecho de Q.
En el gráfico que puede observar que tanto A como B tienen la misma altura (n), y C es una unidad mayor (n+1). Esto hace que el FE de Q sea 1, la altura del subárbol que tiene Q como raíz es (n+2) y por lo tanto el FE de P es 2.
1. Pasamos el subárbol izquierdo del nodo Q como subárbol derecho de P. Esto mantiene el árbol como ABB, ya que todos los valores a la izquierda de Q siguen estando a la derecha de P.
2. El árbol P pasa a ser el subárbol izquierdo del nodo Q.
3. Ahora, el nodo Q pasa a tomar la posición del nodo P, es decir, hacemos que la entrada al árbol sea el nodo Q, en lugar del nodo P. Previamente, P puede que fuese un árbol completo o un subárbol de otro nodo de menor altura.
En el árbol resultante se
puede ver que tanto P como Q quedan equilibrados en cuanto altura. En el caso
de P porque sus dos subárboles tienen la misma altura (n), en el caso de Q,
porque su subárbol izquierdo A tiene una altura (n+1) y su subárbol derecho
también, ya que a P se añade la altura de cualquiera de sus subárboles.
4.2.-GRAFOS
Un grafo G es un par G = (V, E), donde V es un conjunto finito (vértices, nodos) y E es un multiconjunto de pares no ordenados de vértices, denotados por {x, y}, que se denominan lados, aristas, etc. En este caso decimos que X y Y son extremos de {x, y}. Denotamos V (G) por el conjunto de vértices del grafo G y por E (G) el conjunto de lados del grafo G.
Además (G) y "(G) denotan el número de vértices y el número de aristas de G respectivamente. Puesto que E es un multiconjunto es posible que existen pares repetidos, en este caso G tiene lados múltiples. También es posible que algún par no ordenado de E tenga el mismo vértice repetido, en este caso decimos que el lado es un lazo (loop) o bucle. Cuando existen lados múltiples y/o lazos decimos que G es un multígrafo.
Si no hay lados múltiples ni lazos decimos que es un grafo simple. Un dígrafo G es un par G = (V, E) donde V es un conjunto de vértices y E es un multiconjunto de pares ordenados. Los lados se denotan por pares ordenados, (u, v) denota el lado dirigido que tiene como vértice inicial a u y como vértice terminal a v.
A continuación damos unas definiciones:
Definición 1.-Un grafo simple G (V, E) consta de V, un conjunto no vacío de vértices, y de E, un conjunto de pares no ordenados de elementos distintos de V. A esos pares se les llama aristas o lados.
Definición 2.-Un grafo dirigido o dígrafo G = (V, E) consta de un conjunto V de vértices, un conjunto E de aristas, que son pares ordenados de elementos de V.
En matemáticas y ciencias de la computación, un grafo (del griego grafos: dibujo, imagen) es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre elementos de un conjunto. Son objeto de estudio de la teoría de grafos.
Típicamente, un grafo se representa gráficamente como un conjunto de puntos (vértices o nodos) unidos por líneas (aristas). Desde un punto de vista práctico, los grafos permiten estudiar las interrelaciones entre unidades que interactúan unas con otras. Por ejemplo, una red de computadoras puede representarse y estudiarse mediante un grafo, en el cual los vértices representan terminales y las aristas representan conexiones (las cuales, a su vez, pueden ser cables o conexiones inalámbricas).
4.2.1.- TERMINOLOGÍA DE GRAFOS
Dependiendo del tipo de relación entre los vértices del grafo, se definen distintos tipos de grafos. Así se distinguen aristas dirigidas y no dirigidas:
Arista dirigida: es aquella que define un par ordenado de vértices (u, v), donde el primer vértice u es el origen de la arista y el segundo vértice v es el término (o vértice final). El par (u, v) ≠ (v, u).
Arista no dirigida: es aquella que define un par no ordenado de vértices (u, v), donde (u, v) = (v, u).
De esta forma se distinguen entre grafos dirigidos y grafos no dirigidos.
Grafo dirigido: Es aquel cuyas aristas son dirigidas. Los grafos dirigidos suelen representar relaciones asimétricas como por ejemplo: relaciones de herencia, los vuelos entre ciudades, etc.
1. Vértice (Vertex) Un punto o un nodo de un grafo.
2. Arco (Edge) Una línea que un vértice con otro vértice del mismo grafo, en grafos no direccionados, o una fecha que une dos vértices del mismo grafo, en grafos direccionados.
3. Cabeza (Head) En grafos direccionados, es el vértice donde llega la flecha.
4. Cola (Tail) en grafos direccionados, es el vértice desde donde sale la fecha.
5. Vértices Adyacentes (Adjancent Edges) Son dos vértices que están unidos por un arco.
6. Arcos Incidentes (Incident Edges) Son los arcos que inciden en un determinado vértice.
2. Según el tipo y cantidad de arcos
1. Grafo No Direccionado (Undirected Graph) Son grafos donde los arcos unen un par de vértices desordenados. Así, el par (v1,v2) y el (v2,v1) representa el mismo arco.
2. Grafo (Graph) Es un sinónimo de grafo no direccionado. Los grafos no direccionados, normalmente se los llama grafos a secas.
3. Grafo Completo (Completed Graph) Es un grafo no direccionado donde existe un arco entre cada par de vértices cualesquiera del mismo. El número máximo de arcos que puede tener un grafo de n vértices es n * (n - 1) / 2.
4. Grafo Direccionado (Directed Graph) Son grafos donde los arcos unen un par de vértices ordenados. Así, el par [v1, v2] y [v2, v1] representan arcos distintos. En el caso del arco [v1, v2], v1 es la cola del arco y v2 en la cabeza. Los arcos de un grafo direccionado se representan con flechas.
5. Dígrafo (Digraph) Es un sinónimo de grafo direccionado.
6. Digrafo Completo (Completed Digraph) Es un grafo direccionado donde existe un arco entre cada dos vértices cualesquiera del mismo, tanto el que va desde un vértice al otro, como el que retorna. El número máximo de arcos que puede tener un dígrafo de n vértices es n * (n - 1).
7. Multígrafo (Multigraph) Se aceptan más de un arco uniendo dos vértices. En términos formales, no son grafos.
8. Subgrafo (Subgraph) Un subgrafo de G es un grafo G', tal que V(G') está incluido en V(G) y E(G') está incluido en E(G).
3. Según la conectividad
1. Componentes Conectados (Connected Component) Tiene distinto significado según se trate de grafos direccionados o no direccionados.
2. Fuertemente Conectado (Strongly Connected) Tiene distinto significado según se trate de grafos direccionados o no direccionados.
4. Conceptos vinculados al grado.
1. Grado de un Vértice (Vertex Degree) Es el número de arcos que inciden sobre el vértice.
2. Grado Entrante de un Vértice (Vertex In Degree) Es el número de arcos para los cuales el vértice es la cabeza.
3. Grado Saliente de un Vértice (Vertex Out Degree) Es el número de arcos para los cuales el vértice es la cola.
5. Conceptos vinculados al paso
1. Paso (Path) El paso desde un vértice vp a un vértice vq, en un grafo G, es una secuencia de vértices vp, vi1, vi2,..., vin, vq, tal que (vp, vi1), (vi1,vi2), ..., (vin,vq) son arcos en E(G). Si G es un grafo direccionado, el paso consiste de [vp, vi1], [vi1, vi2],..., [vin, vq], arcos en E (G).
2. Paso Simple (Simple Path) Es un paso, donde todos los vértices, excepto, posiblemente, el primero y el último, son distintos.
3. Paso Ciclo (Cycle Path) Es un paso simple, donde el primero y último vértice es el mismo vértice.
4. Longitud del Paso (Path Length) El número de vértices en un paso.
4.2.2.-OPERACIONES BÁSICAS DE LOS GRAFOS
En los grafos, como en todas las estructuras de datos, las dos operaciones básicas son insertar y borrar. En este caso, cada una de ellas se desdobla en dos, para insertar/eliminar vértices e insertar/eliminar aristas.
Insertar vértice
La operación de inserción de un nuevo vértice es una operación muy sencilla, únicamente consiste en añadir una nueva entrada en la tabla de vértices (estructura de datos que almacena los vértices) para el nuevo nodo. A partir de ese momento el grafo tendrá un vértice más, inicialmente aislado, ya que arista llegará a él.
Insertar arista
Esta operación es también muy sencilla. Cuando se inserte una nueva arista en el grafo, habrá que añadir un nuevo nodo a la lista de adyacencia (lista que almacena los nodos a los que un vértice puede acceder mediante una arista) del nodo origen, así si se añade la arista (A,C), se deberá incluir en la lista de adyacencia de A el vértice C como nuevo destino.
Eliminar vértice
Esta operación es inversa a la inserción de vértice. En este caso el procedimiento a realizar es la eliminación de la tabla de vértices del vértice en sí. A continuación habrá que eliminar las aristas que tuviesen al vértice borrado como origen o destino.
Eliminar arista
Mediante esta operación se borra un arco del grafo. Para llevar a cabo esta acción es necesario eliminar de la lista de adyacencia del nodo origen el nodo correspondiente al nodo destino.
Otras operaciones
Las operaciones adicionales que puede incluir un grafo son muy variadas. Además de las clásicas de búsqueda de un elemento o recorrido del grafo, también podemos encontrarnos con ejecución de algoritmos que busquen caminos más cortos entre dos vértices, o recorridos del grafo que ejecuten alguna operación sobre todos los vértices visitados, por citar algunas operaciones de las más usuales.
BIBLIOGRAFIA:
4.1 Arboles
4.1.1 Concepto de árbol
4.1.2 Clasificación de arboles
Rescooped by Cinthia Carrasco from Estructura de Datos
| |
| |
4.1.3 Operaciones básicas sobre arboles binarios
Unidad 4 Arboles y Grafos OAG (Investigacion 2)
Publicado por Osvaldo Apolinar
4.1.4 Aplicaciones
CUARTA UNIDAD- ESTRUCTURAS NO LINEALES | ESTRUCTURA DE DATOS- Rosa Ma. Cristobal Joaquin.
4.1.5 Arboles balanceados (AVL)
4.2 Grafos
4.2.1 Terminología de grafos
4.2.2 Operaciones básicas sobre grafos
DataStructures Tool
Suscribirse a:
Entradas (Atom)